2.6. Pruebas de Hipótesis

Un principio fundamental de la investigación científica y la adquisición de datos por medio de observaciones y experimentos, es que debemos realizar pruebas estadísticas, no para probar si los datos validan nuestra hipótesis, sino para probar la hipótesis nula que invalida la nuestra. En esta sección utilizarán algunas pruebas de hipótesis de uso común:

hipótesis sobre la media de una o dos muestras
hipótesis sobre la independencia de variables categóricas
hipótesis sobre el efecto de factores o tratamientos
hipótesis sobre la relación entre dos variables

2.6.1. Prueba de Hipótesis sobre la Diferencia entre Dos Muestras

Al finalizar esta sección podrás realizar una prueba t e interpretarla

Prueba t para dos muestras

Su uso principal es la comparación de las medias de dos muestra. Asume que las dos muestras provienen de poblaciones con una distribución normal para la variable medida. La hipótesis nula a probar y la alterna son las siguientes: \[H_0 : \mu_a = \mu_b\]
\[H_A : \mu_a \neq \mu_b\] En R esta prueba se puede realizar con la función t.test. A continuación vamos a probar si los efectos de dos drogas, en el tiempo de coagulación sanguínea en conejos, son iguales (\(H_0\)).

#datos
drogaA <- c(8.8,8.4,7.9,8.7,9.1,9.6)
drogaB <- c(9.9,9.0,11.1,9.6,8.7,10.4,9.5)
#prueba
pruebat <- t.test(drogaA,drogaB)
print(pruebat)

## 
##  Welch Two Sample t-test
## 
## data:  drogaA and drogaB
## t = -2.5454, df = 10.701, p-value = 0.02774
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.8543048 -0.1314095
## sample estimates:
## mean of x mean of y 
##  8.750000  9.742857

El valor de p (p-value) es suficientemente bajo (menor de \(\alpha = 0.05\)) para rechazar la hipótesis nula, de que las medias son iguales.

2.6.2. Prueba de Hipótesis sobre la Independencia entre Dos Variables Categóricas

Al finalizar esta sección podrás realizar una prueba de chi-cuadrado e interpretarla

Tabla de contingencia y prueba \(\chi^2\) de independencia

Queremos probar la independencia entre la característica color de pelo y sexo, en 300 humanos, seleccionando al azar 100 hombres y 200 mujeres. En primer lugar, creamos lo que se conoce como una tabla de contingencia:

	color de pelo
sexo	NEGRO	MARRON	RUBIO	ROJO	total
HOMBRE	32	43	16	9	100
MUJER	55	65	64	16	200
total	87	108	80	25	300

La forma más general de plantear las hipótesis es:
\(H_0\): el color del pelo es independiente del sexo en la población muestreada, y
\(H_A\): el color del pelo no es independiente del sexo en la población muestreada.

Con los valores de la tabla de contingencia completa, podemos realizar la prueba \(\chi^2\) en R (chisq.test).

#definimos matriz frecuencias observadas
mfo <- matrix(c(32,43,16,9,55,65,64,16), ncol = 4, byrow = TRUE)
#data frame desde matriz de datos
pelo_sexo <- as.data.frame(mfo)
# prueba
chisq.test(pelo_sexo)

## 
##  Pearson's Chi-squared test
## 
## data:  pelo_sexo
## X-squared = 8.9872, df = 3, p-value = 0.02946

El valor de p (p-value) es suficientemente bajo (menor de \(\alpha = 0.05\)) para rechazar la hipótesis nula, de que el color del pelo y el sexo, son independientes.

Gráfica de mosaico para tabla de contingencia

Ahora bien, la prueba estadística solo nos indica si se acepta o rechaza la hipótesis nula, pero no nos específica dónde están las principales discrepancias entre las frecuencias, por efecto de la no-independencia entre los variables nominales. Una gráfica de mosaico puede ayudarnos a identificar las categorías entre las que se producen las mayores discrepancias.

library(vcd)
mosaic(mfo, shade = TRUE, legend = FALSE, 
       labeling_args = list(set_varnames = c(A = "Sexo", B = "Color Pelo")), 
       set_labels = list(A = c("Hombre","Mujer"), B = c("Negro","Marrón","Rubio","Rojo")))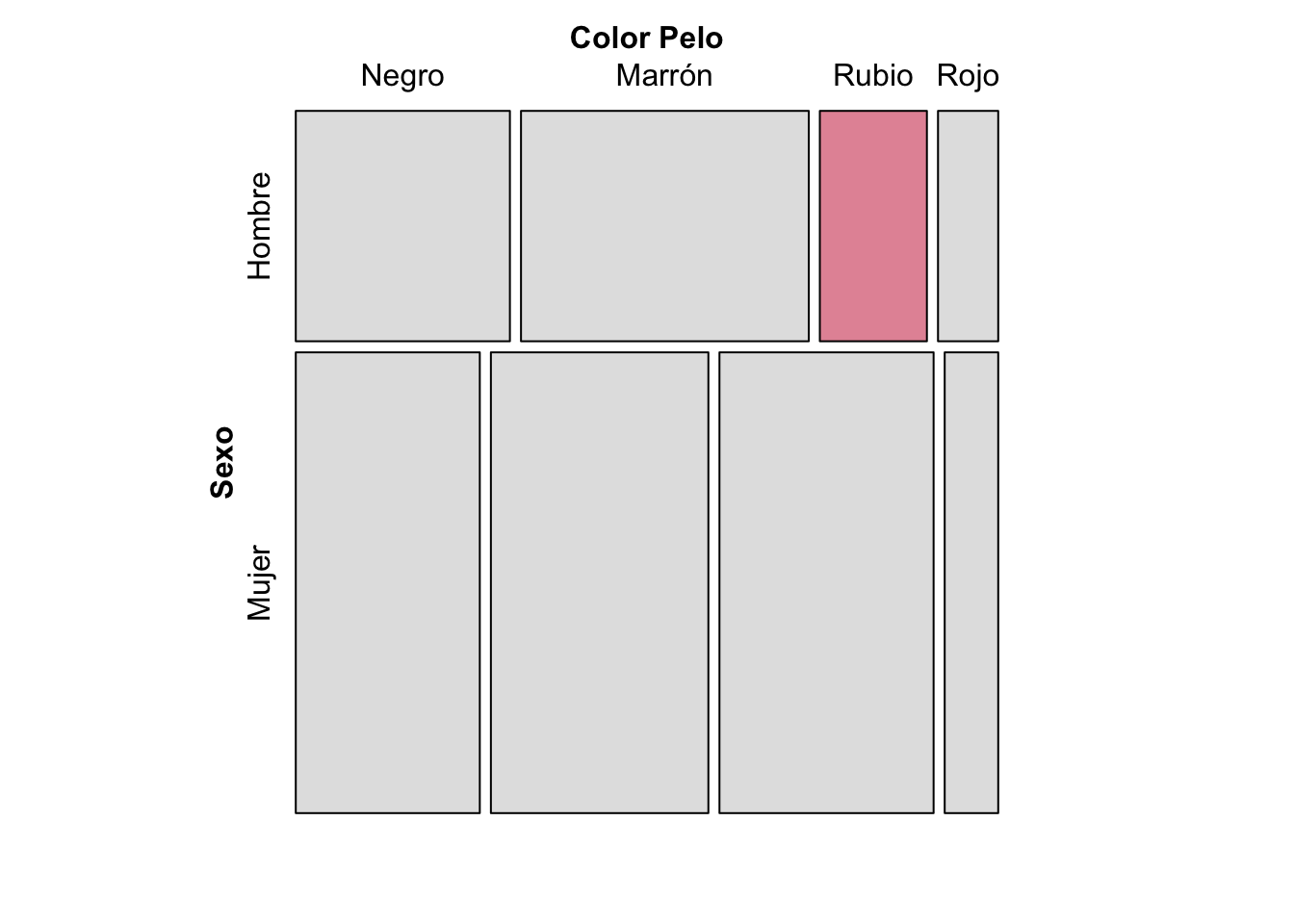

Figura 1 Gráfica de mosaico para la tabla de contingencia sobre la independencia del color del pelo y el sexo. \(\chi^2\) = 8.9872, p-value = 0.02946

2.6.3. Prueba de Hipótesis sobre las Diferencias entre Varias Muestras (Análisis de Varianza)

Al finalizar esta sección podrás realizar un análisis de varianza de un factor (One Way ANOVA) e interpretarlo

En una investigación, 19 cerdos jóvenes fueron asignados, al azar, a cuatro grupos experimentales. Cada grupo se alimentó con una dieta diferente (D1, D2, D3, D4). Luego de ser criados hasta adultos, se midió la masa corporal (kg) de cada animal. Queremos saber si la masa corporal resultó ser igual (\(H_0\)) para las cuatro dietas. \[H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4\] \[H_A: la\ masa\ promedio\ de\ los\ cerdos\ no\ resultó\ igual\ en\ todas\ las\ dietas.\]

# datos
D1 <- c(60.8,67,65,68.6,61.7)
D2 <- c(68.7,67.7,75,73.3,71.8)
D3 <- c(69.6,77.1,75.2,71.5)
D4 <- c(61.9,64.2,63.1,66.7,60.3)
#tabla de datos - creación de lista
cerdos <- list(Dieta_1 = D1, Dieta_2 = D2, Dieta_3 = D3, Dieta_4 = D4)
# ajuste por n diferente de cada tratamiento
cerditos <- as.data.frame(lapply(cerdos, `length<-`, max(sapply(cerdos, length))))
cerditos

##   Dieta_1 Dieta_2 Dieta_3 Dieta_4
## 1    60.8    68.7    69.6    61.9
## 2    67.0    67.7    77.1    64.2
## 3    65.0    75.0    75.2    63.1
## 4    68.6    73.3    71.5    66.7
## 5    61.7    71.8      NA    60.3

Visualización de los tratamientos con gráficas de box&whisker

# arreglo de datos en un data frame
#data frame de dos columnas con factor Dieta
df.cerdos <- data.frame(Dieta=c(rep("D1", times=length(D1)),
                        rep("D2", times=length(D2)),
                        rep("D3", times=length(D3)),
                        rep("D4", times=length(D4))),
                   masa=c(D1, D2, D3, D4))
# box-plot para cada tratamiento
library(ggplot2)
ggplot(df.cerdos, aes(x=Dieta, y=masa)) +
  geom_boxplot(fill="cornflowerblue") +
  stat_summary(fun=mean, geom="point", shape=10, size=5,
               color="red", fill="red") +
  labs(x = "Dietas", y = "Masa corporal, kg")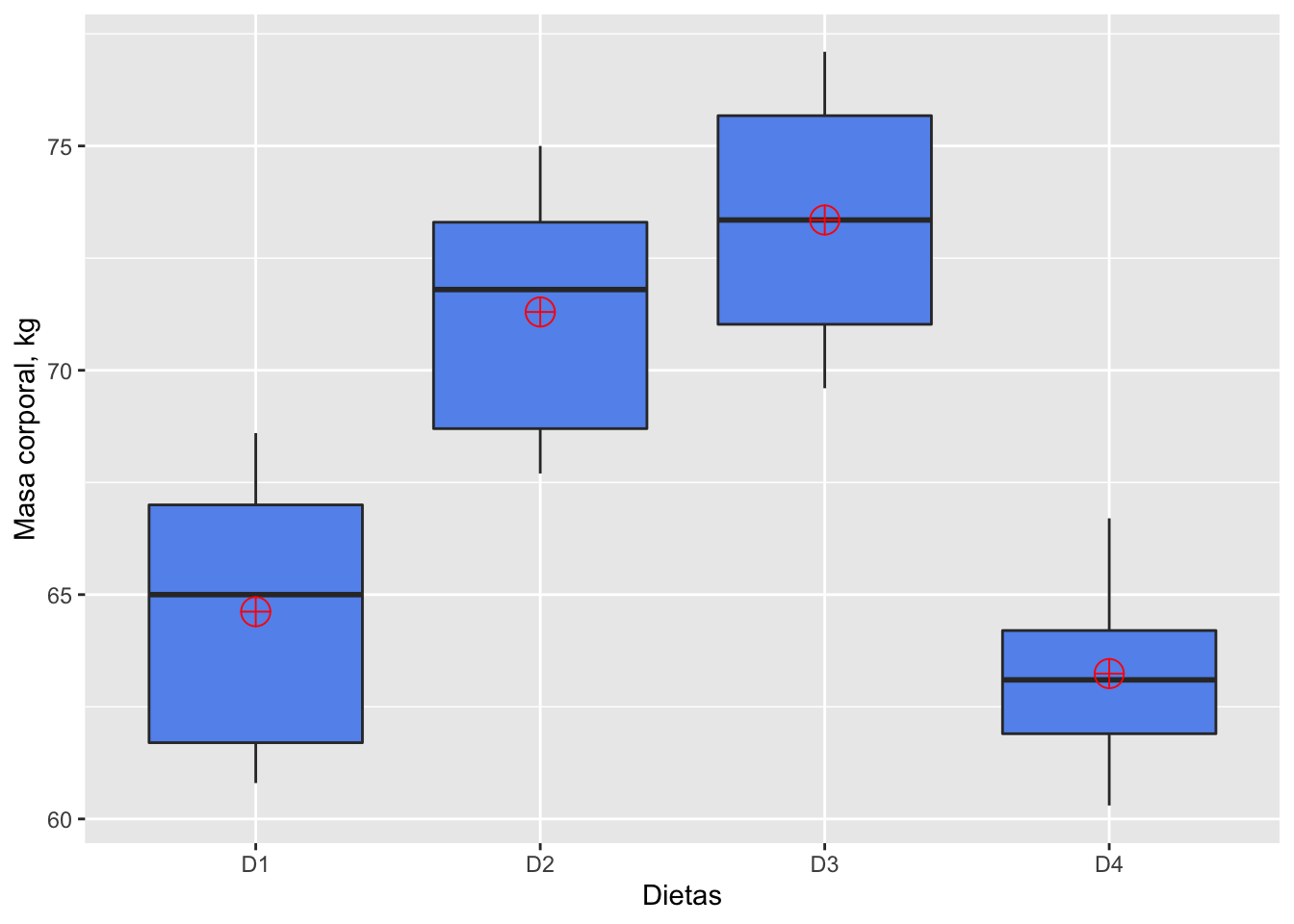

Figura 2 Gráficas de box&whisker de la masa corporal (kg), de cuatro grupos de cerdos (n =4,5), luego de estar en cuatro dietas diferentes.

Estadísticos del análisis de varianza

analisis <- aov(masa ~ Dieta, df.cerdos)
summary(analisis)

##             Df Sum Sq Mean Sq F value   Pr(>F)    
## Dieta        3  338.9  112.98   12.04 0.000283 ***
## Residuals   15  140.8    9.38                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

El valor de P para el estadístico F (Pr(>F)) es significativo para rechazar la hipótesis nula. Sin embargo, este análisis no nos indica cuál o cuáles tratamientos son diferentes entre sí, para esto hay que realizar pruebas post-hoc, como la prueba Tukey.

2.6.4. Prueba de Hipótesis sobre la Relación entre dos Variables (Análisis de Regresión)

Al finalizar esta sección podrás realizar una análisis de regresión lineal simple e interpretarlo

Una regresión lineal simple modela el efecto de una variable predictora continua sobre una variable de respuesta continua. La ecuación de regresión resultante se puede representar gráficamente como una línea de regresión, que representa los valores esperados de la variable de respuesta para todos los valores de la variable predictora.

En la regresión lineal simple, la relación funcional entre la variable dependiente (y) y la independiente (x) se representa:
\[\mu_y = \alpha + \beta x\]

donde:

\(\mu_y\): es la media poblacional de y para cualquier valor de x,
\(\alpha\): es el intercepto y
\(\beta\): es la pendiente.

Tenemos datos de individuos entre 21 y 79 años, a los cuales se le midió el perímetro a nivel de la cintura y la concentración plasmática de triglicéridos, y establecimos un modelo de regresión, en el cual el nivel de triglicéridos depende del valor de cintura. Vamos a probar si la pendiente de la ecuación de regresión tiene un valor diferente de 0, por lo tanto nuestra hipótesis nula será:
\[\beta = 0\]

# datos
trigli <- read.csv("data/triglicerido.csv")
# gráfica exploratoria
plot(trigli$cintura, trigli$trigliceridos,
     xlab = "Cintura, pulgadas", ylab = "Triglicéridos en sangre, mg/dl")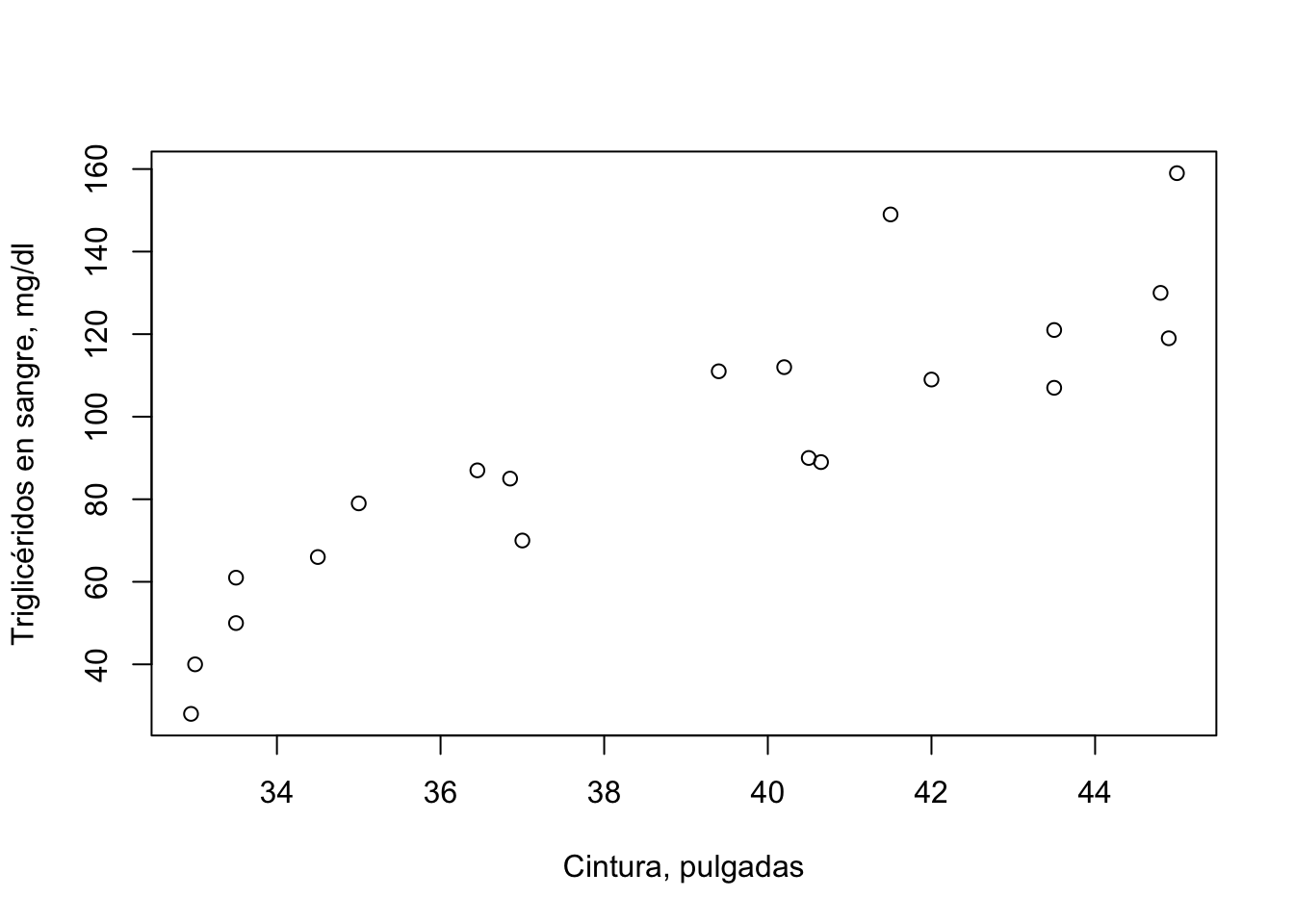

Figura 3 Triglicéridos en sangre (mg/dl) en relación al perímetro de la cintura (pulgadas), en individuos entre 21 y 79 años.

Análisis de regresión lineal simple

regrtest <- lm(trigliceridos ~ cintura, data = trigli)
summary(regrtest)

## 
## Call:
## lm(formula = trigliceridos ~ cintura, data = trigli)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -21.814 -11.236  -4.454  10.281  37.349 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -188.4947    33.3154  -5.658 2.29e-05 ***
## cintura        7.2324     0.8508   8.501 1.02e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.94 on 18 degrees of freedom
## Multiple R-squared:  0.8006, Adjusted R-squared:  0.7895 
## F-statistic: 72.27 on 1 and 18 DF,  p-value: 1.021e-07

alfa <- regrtest$coefficients[1]
alfa <- round(alfa[[1]], digits = 2)
beta <- regrtest$coefficients[2]
beta <- round(beta[[1]], digits = 2)

La ecuación de regresión será:

Triglicéridos = -188.49 + 7.23*cintura

Gráfica de la línea de regresión y el intervalo de confianza

library(ggplot2)
ggplot(data=trigli, aes(x=cintura, y=trigliceridos)) +
  geom_point(pch=19, color="blue", size=2) +
  geom_smooth(method="lm", color="red", linetype=2) +
  labs(x="Cintura, pulgadas", y="Triglicéridos en sangre, mg/dl")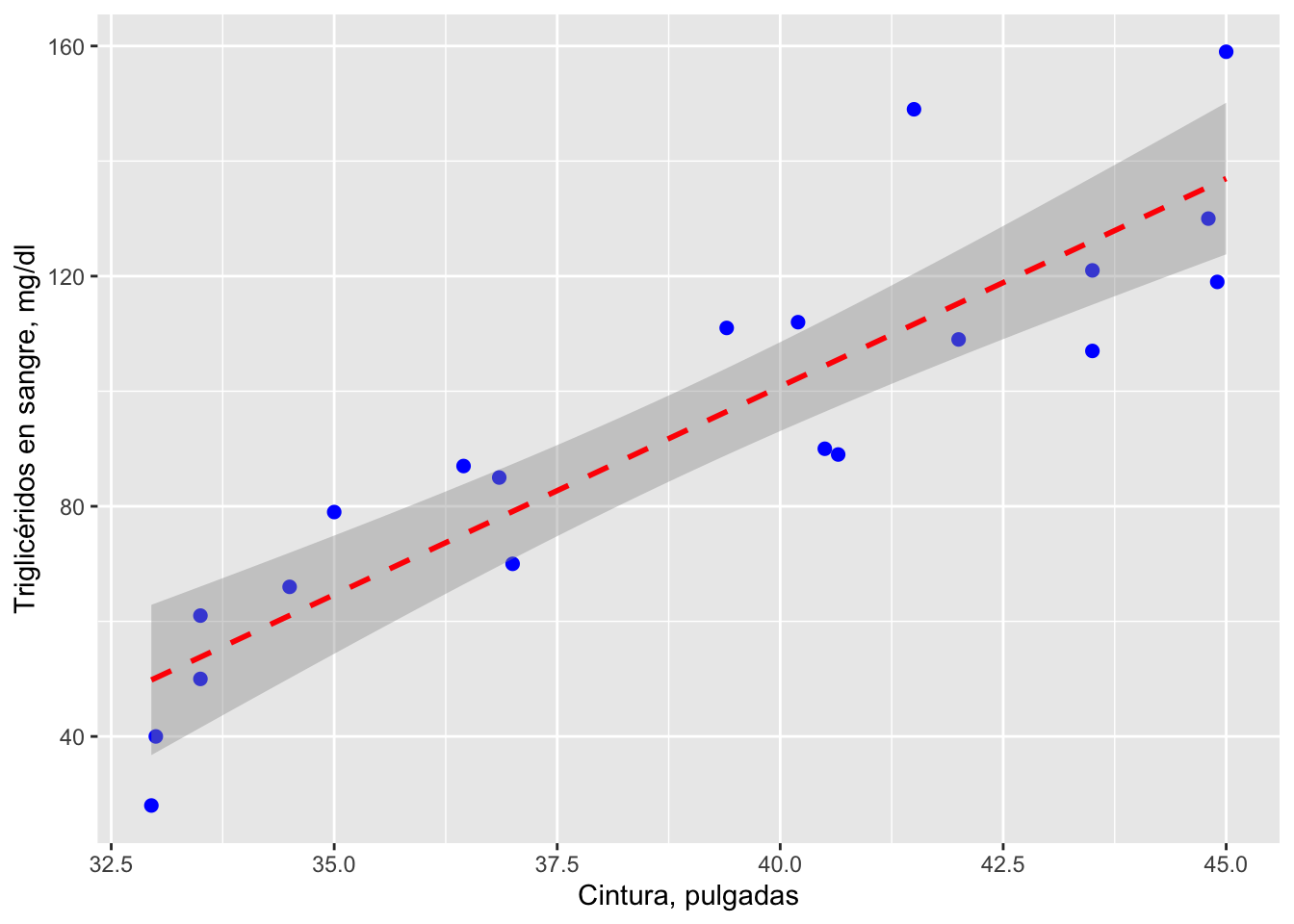

Figura 4 Línea de regresión e intervalo de confianza (95%) para la relación entre el nivel de triglicéridos en la sangre y el perímetro de la cintura.